Geometric Integration
Collaborators:
Prof. Robert McLachlan
Massey University, New Zealand
Prof. Sebastian Reich
Universität Potsdam, Germany
Prof. Constance Schober
University of Central Florida
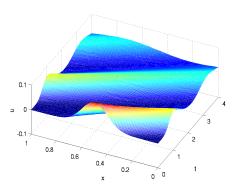
Geometric integration is a term used to describe numerical algorithms for approximating solutions of differential equations. The main idea is to exactly preserve important geometric properties of the equation in order to produce accurate approximations. My work in this field has focused on methods that preserve a multi-symplectic conservation law for Hamiltonian partial differential equations. Equations that commonly fall under this framework are Korteweg-de Vries, Boussinesq, Schrodinger, nonlinear wave equations, and many others. My work in this field has helped explain some of the conservation properties of these schemes through the derivation of discrete conservation laws and through the development and use of backward error analysis. I am currently conducting research focusing on additional structure-preserving properties for methods applied to equations with added dissipation and equations with traveling wave solutions. Research Students: Laura Norena, Ashish Bhatt, and Dwayne Floyd
Traveling Waves
Collaborators:
Prof. Tony Humphries
McGill University, Canada
Prof. Erik VanVleck
University of Kansas
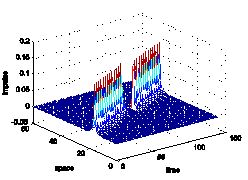
Traveling wave solutions for differential equations have a large range of applications. My work on this topic has focused on spatially discrete bistable equations which are mathematical models for crystal growth or electrical impulses traveling in the nervous system. With my collaborators, we have derived exact solutions for a problem in which the waves propagate, or fail to propagate, in discrete media that are inhomogeneous on an interval. Using Jacobi operator theory, we have derived necessary and sufficient conditions for propagation failure of waves due to inhomogeneities, and using transform techniques we find changes in wave speed and wave form as waves pass through inhomogeneities. Since our results for this problem are exhaustive, and they are the first to give exact solutions for waves propagating in discrete inhomogeneous media, they have naturally opened the door to new problems and further research in the field. Research Students: Lory Ajamian, Jonathan Fraine, Jessica Long, Nicole Lopez, Joe Segal and Johann Veras.
Computer Vision

Collaborators:
Prof. Mubarak Shah
UCF Center for Research in Computer Vision
Computer vision research concerns development of algorithms, enabling computers to recognize features of digital images or video sequences. My research in this field has solved problems in both action recognition and crowd scene understanding, using several techniques and ideas and from differential equations theory. Specifically, we have used stability analysis for differential equations, based on the eigenvalues of the Jacobian matrix from linearization, to recognize behaviors of crowds, such as bottlenecks, lane formation, and blocking or clogging. We have also used a Lagrangian approach to fluid dynamics and a streakline representation for flow to recognize changes in flow in crowded scenes, with applications to segmentation of motion and recognition of abnormal behaviors in crowds. Research Students: Ramin Mehran, Berkan Solmaz.
Granular Mechanics

Figure: Metzger, Philip T. Rocket Exhaust Cratering: A Significant Challenge for Space Exploration.
24 March 2010
Collaborators:
Dr. Philip T. Metzger
NASA, Kennedy Space Center
Granular mechanics is concerned with understanding the physics behind motion in granular beds. My work in this field is supported by NASA, and we are working to understand the effects of rocket exhaust on soil. Our specific focus is on finding conditions that are sufficient for crater formation. Physical experiments are limited in this research, because we currently have no way to accurately test rockets in planetary environments other than our own. As a result, we are using a system of partial differential equations as a model for soil/rocket exhaust interaction, and solving them numerically provides predictions of when and how soils will develop craters under various conditions. Comparing our results to physical experiment helps verify our simulations, and predictions made by our model, for environments where data is unavailable, will help NASA make important decisions about building landing pads for future space missions. Research Students: Brian W. Brennan, Kristina Kraakmo, Whitney Keith.