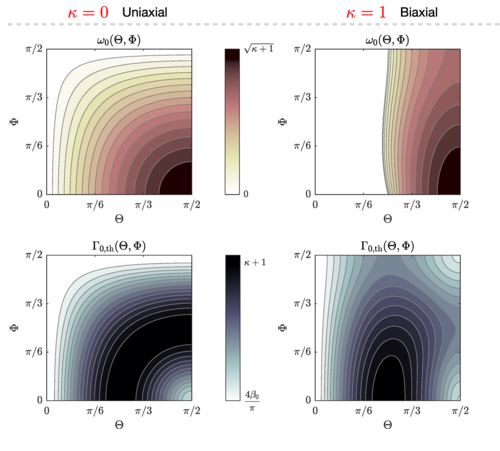
The Néel order of an antiferromagnet subject to a spin torque can undergo precession in a circular orbit about any chosen axis. The direction of the axis uniquely determines the component of spin polarization in the orbital plane required for that particular axis orientation as well as the perpendicular component of spin polarization required for stability of the precessional motion. For biaxial antiferromagnets, the orbital angular motion reduces to equation of a damped-driven pendulum, which has hysteresis versus the spin-current drive with a critical value where the period diverges. The fundamental frequency of the motion varies inversely with the damping. The stability threshold for spin current has an approximate closed-form result, which depends on the minimum cutoff frequency the orbit can support, and the damping-anisotropy parameters. The direction along the hard axis has zero cutoff frequency and the lowest threshold, and the easy axis has the highest cutoff frequency. A device setup is proposed for electrical control and detection of the dynamics, which is promising for terahertz nano-oscillators. This work has been published in PRB and can be accessed here.