Quantum processing machines can, in principle, seriously outperform some of our current information technologies. For instance, anyone possessing a computer capable of implementing a quantum factoring algorithm will gain virtual access to most secure communications as well as databases. Moreover, quantum entanglement can also be used to avoid any eavesdropping in communications. This has led to an intense effort to build quantum processors and quantum communication devices. However, in practice, processing information remains a challenging task. It is still not clear which physical system is most suitable for implementing quantum computation at large scales. In addition, one needs not only full control and the possibility for large-size scaling, but also to cope with errors and imperfections, as quantum systems are very susceptible to noise coming from their environment.
Michael Leuenberger
Leuenberger and his group develop theoretical work on these fronts. They study quantum bits made from quantum dots in 3D topological insulators (3DTI), which host topologically protected states on their surface. In particular, they consider bound states of Weyl fermions, which are localized on the surface of a 3DTI quantum dot. Strict optical selection rules allow for controlled entanglement between single photons and localized spins on the 3DTI quantum dots, paving the way to optically mediated quantum communication and quantum computing with 3DTI quantum dots.
Eduardo Mucciolo
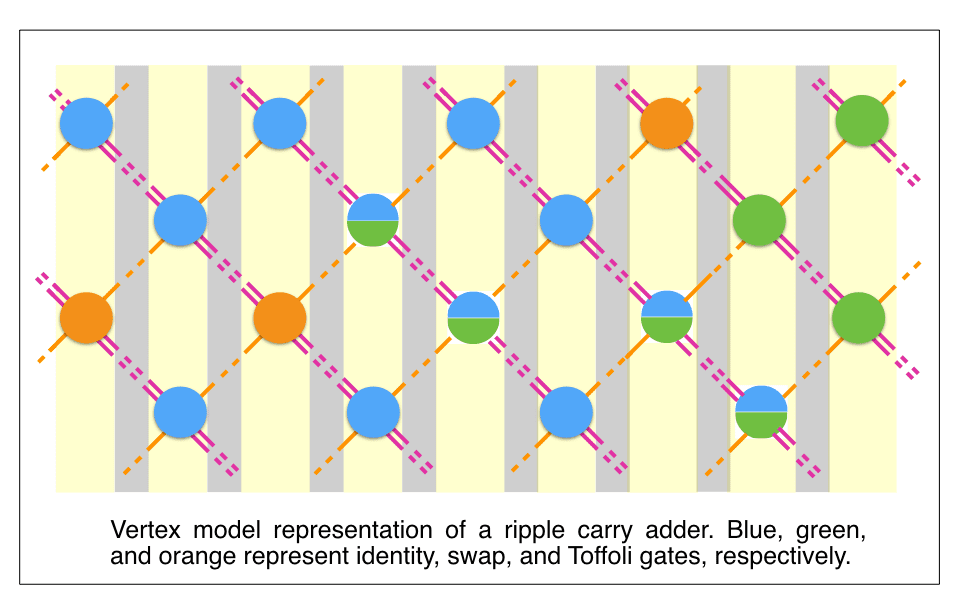
Mucciolo and his group explore the physical limits of quantum computation and ways to mitigate the noise problem. They have developed a theoretical framework to study the limitations imposed by the environment on topological quantum memories, and in particular the surface code, which is one of the most promising ways to encode and protect quantum information. In parallel to their research in quantum information, they look at ways to use computational tools developed in the study of quantum many-body systems to tackle hard combinatorial problems. For that purpose, they have developed novel methods based on matrix product states and tensor networks, and have proposed ways of mapping circuit problems onto statistical models.